DEFINIZIONE ASSIOMATICA DI PROBABILITA' CONDIZIONATA

Come abbiamo visto, a volte il sapere che un evento A si è verificato può costituire un'informazione che modifica la misura di probabilità per un altro evento B. Come sappiamo, si parla allora di probabilità condizionata.  Nell'impostazione assiomatica, la probabilità condizionata viene definita dalla seguente formula:

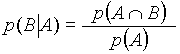
Tale definizione ha una interpretazione intuitiva: si tratta infatti di una "nuova" funzione di probabilità, definita all'interno del solo insieme A, sottospazio dell'universo. Ovviamente p(B|A) perde di senso se p(A)=0.

Quando p(B|A)> p(B) si dice che gli eventiA e B hanno una correlazione positiva, cioè l'informazione che A si è verificato ha aumentato la probabilità di B.
Quando p(B|A)< p(B) si dice che gli eventiA e B hanno una correlazione negativa, cioè l'informazione che A si è verificato ha diminuito la probabilità di B.

Esempio: lanciamo due dadi e consideriamo gli eventi
A: "la somma dei due numeri è 6"
B:" i due numeri sono dispari"
Qual è la probabilità che i due numeri siano dispari, sapendo che la loro somma è 6?

Poiché: p(A)=5/36; p(B)=9/36; p(AÇ B)=3/36, troviamo, applicando la definizione vista:
p(B|A)=3/5.
Notiamo che abbiamo ristretto l'universo iniziale di 36 casi possibili al sottoinsieme A comprendente solo 5 casi. Di questi, solo 3 sono favorevoli.

In una famiglia con due bambini, un bambino è maschio. Qual è la probabilità che l'altro bambino sia una femmina?

Questo problema merita uno sguardo da vicino...

Nell'esempio appena visto, p(B|A) > p(B); diremo quindi che i due eventi sono correlati positivamente. Effettivamente possiamo verificare che anche p(A|B) > p(A) : applicando nuovamente la definizione si ha p(A|B)=1/3.

TEOREMA DELLA MOLTIPLICAZIONE

Dalla definizione di probabilità condizionata discende immediatamente il teorema della moltiplicazione:

Esempio: un'urna contiene 5 palline numerate da 1 a 5. Si estraggono successivamente due palline, senza rimettere la prima pallina estratta nell'urna (si parla in questi casi di estrazione senza reimmissione). Consideriamo gli eventi
A: "la prima pallina estratta è dispari"
B: "la seconda pallina estratta è dispari"
Qual è la probabilità che entrambe le palline siano dispari?

Applicando il teorema della moltiplicazione, con p(A)= 3/5, p(B|A)=2/4, troviamo
p(AÇ B)=(3/5)(2/4)=6/20.

Se gli eventi A e B sono indipendenti, p(B|A)=p(B) e come conseguenza diretta del teorema della moltiplicazione troviamo:

Se nell'esempio precedente rimetto la prima pallina estratta nell'urna, prima di estrarre la seconda (si parla in questi casi di estrazione con reimmissione), la seconda estrazione è ovviamente indipendente dalla prima (a meno di ritenere che le urne abbiano una "memoria") e troviamo:
p(entrambe dispari)=(3/5)(3/5)=9/25.

L'ultima formula può anche essere utilizzata come test di indipendenza stocastica tra eventi: infatti se
è verificata, dal teorema della moltiplicazione avremo che p(B|A)=p(B) e gli eventi A e B sono indipendenti.