Géométrie du plan : Frises et Pavages
Géométrie du plan : Frises et Pavages
La première partie de ce document est conçue comme une initiation à la géométrie du plan et une introduction à l'utilisation des groupes. Ce travail mène naturellement à l'étude des frises (ou ornement linéaires) et des pavages, ce que nous faisons ici.
Il a été développé au fil d'un cours d'ouverture à l'intention d'étudiants de L1 et L2 comme une promenade dans la géométrie du plan. Il doit beaucoup à des documents que m'a donnés Daniel Perrin lors de la préparation de ce cours.

Le plan affine est noté .
I Frises
Géométrie du plan : Frises et Pavages
→ I Frises

Pour analyser une frise, il faut
- déterminer la bande, c'est-à-dire la direction des translations et un motif de translation ;
- trouver son groupe ponctuel, les directions des axes de réflexion, l'ordre des rotations ;
- placer les éléments de symétrie (centres de rotation, axes de réflexion, axes de réflexion glissée).
- déterminer le groupe de ses isométries parmi une liste finie que nous allons donner.
- déterminer un motif de base.
Faisons d'abord l'étude mathématique.
I-2 Groupe discret, groupe ponctuel
Géométrie du plan : Frises et Pavages
→ I Frises
I-1 Ornement linéaire
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-1 Ornement linéaire
Prenons une bande
, c'est-à-dire la zone du plan comprise
entre deux droites parallèles et un dessin dans cette bande, c'est-à-dire
un sous-ensemble de la bande ou un dessin coloré (un nombre fini de sous-ensembles
disjoints de cette bande) contenu dans un parallélogramme et translatons-le
dans la direction de la bande de manière à ce qu'il n'y ait pas de superposition, on obtient
une frise.
Définition
Un ornement linéaire ou frise est
un dessin
de
dont le groupe des translations
de
est de la forme
où
est
un vecteur non nul.
Définition
Un motif de translation
est une partie fermée de
, connexe (c'est-à-dire d'un seul
morceau) telle que les translatés de
par les translations de
recouvrent
:
et telle que l'intersection de deux tels translatés soit contenue dans leur
frontière.
Un motif de base
est une partie fermée de
, connexe, telle que les images de
par les isométries de
recouvrent
:
et telle que l'intersection de deux tels transformés soit contenue dans leur
frontière.
Par exemple, un parallélogramme de longueur (dans la direction de la bande) la norme de
est un motif de translation. Par contre, le motif de base dépend de la structure du groupe des
isométries.
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-1 Ornement linéaire
I-2 Groupe discret, groupe ponctuel
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-2 Groupe discret, groupe ponctuel
Définition
Un groupe de symétrie d'un ensemble
est discret
s'il existe des réels strictement positifs
et
tel que
- pour toute translation de vecteur non nul appartenant à , ;
-
pour toute rotation d'angle
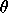 appartenant à
,
.
appartenant à
,
.
Proposition
Si
est discret et laisse fixe un point
, il est fini.
Proposition
Le groupe d'un ornement linéaire est discret.
Proposition
Soit
un point de
.
Le groupe ponctuel
d'un ornement linéaire est fini.
Désormais, est un ornement linéaire dont le groupe des translations de est de la forme avec un vecteur non nul. On fixe une origne du plan.
Proposition
Soit
la droite vectorielle de direction
et
la perpendiculaire à
passant par
.
Tout élément de
est de la forme
où
est une translation et
Autrement dit, le groupe ponctuel
de
est contenu dans le groupe
.Démonstration
Soit
et écrivons
avec
une isométrie
fixant l'origne et
un vecteur.
L'isométrie transformée de par est égale à . Comme appartient à , aussi ; donc . Comme et ont même norme, est ou .
La droite vectorielle de direction est donc stable par ; il en est de même de sa perpendiculaire ( conserve des angles). Donc, peut être : l'identité, la symétrie centrale par rapport à , la réflexion axiale par rapport à ou la réflexion axiale par rapport à .
L'isométrie transformée de par est égale à . Comme appartient à , aussi ; donc . Comme et ont même norme, est ou .
La droite vectorielle de direction est donc stable par ; il en est de même de sa perpendiculaire ( conserve des angles). Donc, peut être : l'identité, la symétrie centrale par rapport à , la réflexion axiale par rapport à ou la réflexion axiale par rapport à .
Les sous-groupes de sont faciles à décrire. Il y en a cinq ;
-
;
-
;
-
;
-
;
-
.
Exercice
Quel est le groupe ponctuel de chacune des frises suivantes :
Voir aussi Groupe ponctuel d'une frise
Voir aussi Groupe ponctuel d'une frise
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-2 Groupe discret, groupe ponctuel
I-3 Droite affine invariante de la bande
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-3 Droite affine invariante de la bande
Proposition
Il existe au moins une droite affine
parallèle à
invariante par
.
Démonstration
Les droites invariantes par le groupe des translations
de
sont les droites de direction
. Nous allons donc chercher la droite
parmi
ces droites. Elle doit être invariante par les isométries de
qui ne
sont pas des translations.
Prenons une isométrie de qui n'est pas une translation. Elle s'écrit
avec
,
,
avec
de direction
et
perpendiculaire à
.
Faisons quelques remarques sur les isométries que l'on peut obtenir
et les droites qu'elles laissent invariantes :
Reprenons maintenant les cinq cas de groupes ponctuels possibles.
Prenons une isométrie de qui n'est pas une translation. Elle s'écrit
- : est une symétrie centrale de centre un point ; toute droite passant par et de direction est invariante par ;
-
avec
droite
de direction
et
parallèle à
(réflexion ou symétrie glissée) ;
on a alors
. Donc
est un multiple de
.
La droite
est stable par
.
-
avec
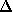 droite
de direction
et
parallèle à
droite
de direction
et
parallèle à
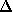 ;
on a alors
. Donc
appartient à
; comme il
est perpendiculaire à
, il est nul. Autrement dit,
est une réflexion d'axe
;
on a alors
. Donc
appartient à
; comme il
est perpendiculaire à
, il est nul. Autrement dit,
est une réflexion d'axe
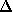 perpendiculaire à
.
Toute droite de direction
est stable par
.
perpendiculaire à
.
Toute droite de direction
est stable par
.
Reprenons maintenant les cinq cas de groupes ponctuels possibles.
-
: toute droite de direction
est invariante par
.
-
;
est engendré par
et par
pour
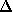 une droite de direction
; toute droite de direction
est invariante par
.
une droite de direction
; toute droite de direction
est invariante par
.
-
; toute droite de direction
est invariante par
.
-
; il y a dans
une réflexion
ou une symétrie glissée
d'axe une droite
de direction
. Cette droite est invariante par les
translations de
et par
donc par
.
-
;
est engendré par
et par
,
et
avec
parallèle à
,
une droite de direction
,
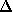 perpendiculaire à
et
un point. Montrons que la droite
est stable par
:
il reste à montrer que
est stable par
(pour les autres, on
utilise les cas précédents). Pour cela, il suffit de montrer que
appartient
à
. L'isométrie suivante appartient à
:
avec parallèle à
perpendiculaire à
et
un point. Montrons que la droite
est stable par
:
il reste à montrer que
est stable par
(pour les autres, on
utilise les cas précédents). Pour cela, il suffit de montrer que
appartient
à
. L'isométrie suivante appartient à
:
avec parallèle à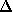 .
Son carré est égal à
et
. Donc
et
.
.
Son carré est égal à
et
. Donc
et
.
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-3 Droite affine invariante de la bande
I-4 Classification
Géométrie du plan : Frises et Pavages
→
I Frises
→ I-4 Classification
Théorème
Il y a exactement 7 groupes de symétrie d'ornements à conjugaison près
par une similitude.
On choisit une droite